Sea la función de utilidad tipo multiplicativa* de un consumidor representativo:

* Esta función es conocida como la función Cobb-Douglas en honor a dos economistas que la usaron para efectuar investigaciones económicas. Esta función es usada normalmente en la función de producción para efectuar análisis siguiendo la teoría del crecimiento.

U = X^a Y^b

y su restricción presupuestal:

I = X P_x + Y P_y

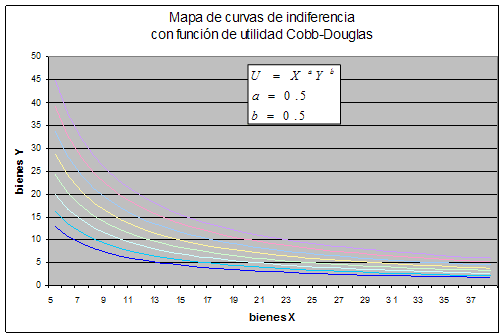
Si se simulan datos hipotéticos de una función de utilidad Cobb – Douglas en una hoja de cálculo obtenemos el gráfico de arriba donde se pueden apreciar una serie de curvas de indiferencia utilizando la función y parámetros que se señalan en el mismo gráfico y las respectivas cantidades de los bienes “X” e “Y”.

Continuando con el análisis y dado el principio del consumo óptimo, tenemos que:

( ∂U / ∂X ) / ( ∂U / ∂Y ) = Umg_x / Umg_y = P_x / P_y

y aplicando este principio a la función de utilidad anterior, tenemos que:

aX ^a-1Y^b / bX^a Y^b-1 = P_x / P_y

resolviendo

aY/bX = P_x/P_y

y reemplazando en la restricción presupuestal, obtenemos la función de la demanda de ambos bienes:

X=[a/(a+b)](I / P_x)

Y=[b/(a+b)](I / P_y)

si efectuamos algunos arreglos:

X.P_x/I = a/(a + b)

Y.P_y/I = a/(a + b)

observamos que la proporción del gasto de cada uno de los bienes respecto al ingreso nominal depende de los coeficientes “a” y “b”. Es decir, la proporción del gasto del bien “X”, es igual que la proporción del coeficiente “a” respecto a la suma de los coeficientes “a “ y “b”; y la proporción del gasto del bien “Y”, es igual que la proporción del coeficiente “b” respecto a la suma de los coeficientes “a “ y “b”

Si los coeficientes “a” y “b” suman la unidad, entonces las proporción del gasto de “X” e “Y” es igual al coeficiente “a” y “b”, respectivamente.

Las funciones inversas de la demanda serán las siguientes:

P_x = a/(a+b) I/X

P_y = b/(a+b) I/Y

si derivamos ambas funciones, tenemos que:

dP_x/d_x= -a/(a+b) (I/X²)

dP_y/d_y= -b/(a+b) (I/Y²)

dichas ecuaciones nos dan la información que las curvas de demanda tiene pendiente negativa; y las segundas derivadas:

d²P_x / d_x² = 2a/(a+b) (I/X³)

d²P_y / s_y² = 2b/(a+b) (I/Y³)

nos dan la información que dichas curvas son cóncavas hacia arriba

Autor: O. Jack Ocrospoma Huerta